Reasoning Dices questions with answer
Dice is a cube having different numbers on all its faces. The numbers are usually a single digit, from 1 to 6.
Numbers on a die:
The scheme of numbering on a die is specific. The sum of the number on the opposite faces will be equal to ‘7’ always. The number 1 will be opposite to number 6. The number 2 is opposite to 5 and 3 is opposite to 4.
Such that:
A.1 + 6 = 7
B. 2 + 5 = 7
C. 3 + 4 =7.
Classification of dice:
There are two types of dice:
- Standard dice
- Ordinary dice
1.standard dice
When the dice are rolled, if the number on the faces of the two dice do not match each other, they are called as standard dice.
2.ordinary dice
If one or more than one number matches between two dice than it is called as an ordinary dice.
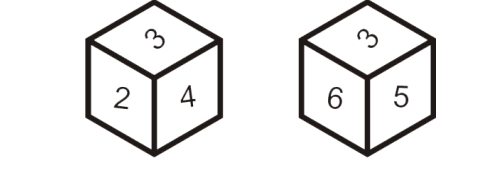
In the above dice, the number ‘3’ is common in both the dice.
In an open dice all the six faces of the dice are shown. The dices show the opposite position of rows and columns.
Example :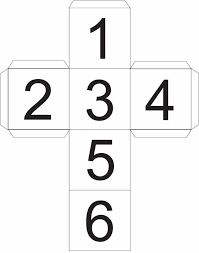
Constructed and Deconstructed Dice:
Constructed Dice :
This section of dice gives the constructed version of dice, the questions will be based on the visualization of the flattened-out version of dice.
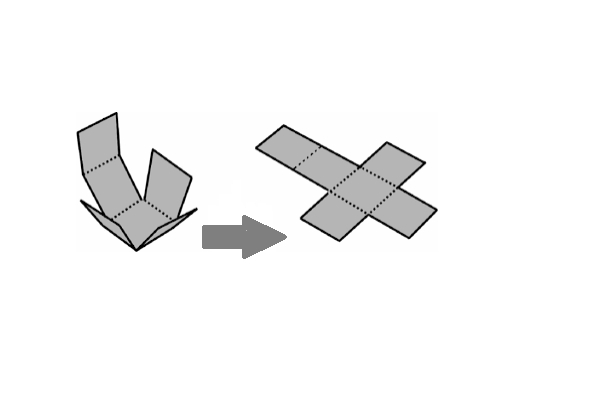
Deconstructed Dice :
This section of dice gives the flattened-out version of dice, the questions will be based on the visualization of what is at the other end of the constructed dice.
Rule No. 1:
Two opposite faces cannot be adjacent to one another.
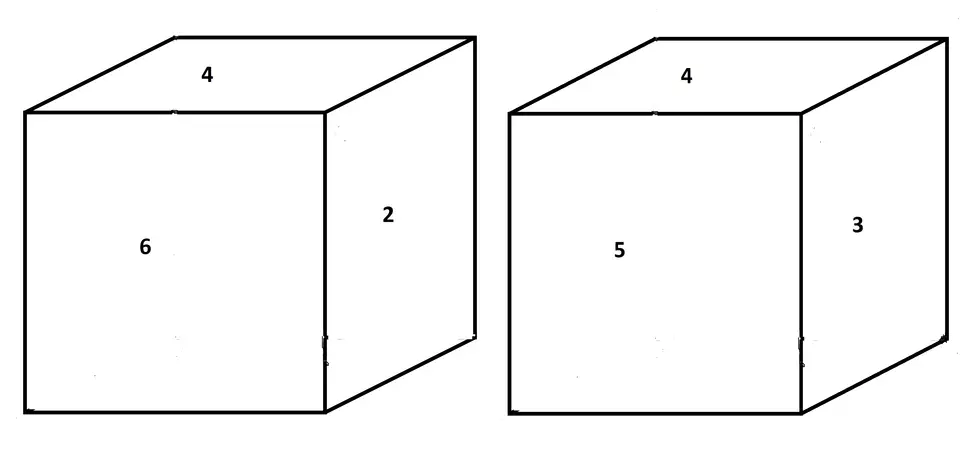
Example:Two different positions of a dice are shown below. Which number will appear on the face opposite to the face with number 4?
Solution:
Faces with four numbers 6, 2, 5 and 3 are adjacent of to the face with No. 4.
the faces with no. 6, 2, 5 and 3 cannot be opposite to the face with no. 4.
Hence 1 is the opposite of number 4.
Rule No. 2:
If two different positions of a dice are shown and one of the two common faces is in the same position then of the remaining faces will be opposite to each other.
Example:Two different positions of a dice are shown below.
Here in both shown positions two faces 5 and 3 are common.
The remaining faces are 2 and 4.
Hence the number on the face opposite to the face with number 2 is 4.
Rule No. 3:
If in two different positions of dice, the position of a common face be the same, then each of the opposite faces of the remaining faces will be in the same position means the opposite of the number on 1st position of dice is same face on the 2nd position of a dice.
Example:Here in both positions of common 3 is same.
Therefore, opposite of 5 is 6 and opposite of 4 is 2.
Rule No. 4:
If in two different positions of a dice, the position of the common face be not the same, then opposite face of the common face will be that which is not shown on any face in these two positions. But, the opposite faces of the remaining faces will not be the same.
Some important Rules for Dice :
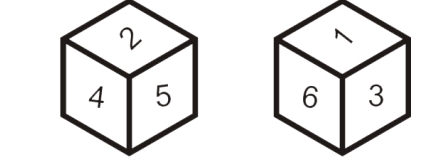
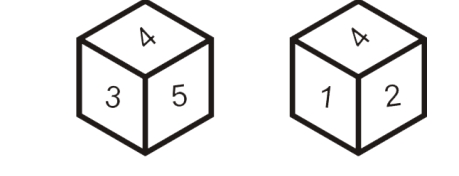
Rule -1:If one of the numbers is common in both the dice when two dice have the same surface, then the remaining surfaces of both dice are opposite to each other.
In the above two dice, the number 4 is common and the numbers 3 and 5 on one die and 1 and 2 on the surface of the other die are opposite to each other respectively. I.e. The number 3 is opposite 1 and 5 is opposite to 2.
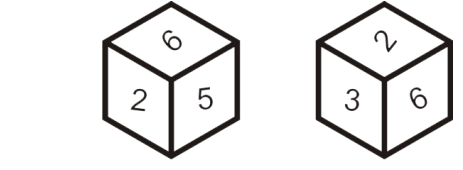
If any two numbers are the same in two dices irrespective of their position on the dice then the remaining third number in both the dice are opposite to each other.
In the above scenario, irrespective of their place or position the two numbers 6 and 2 are common in both the dice. Then the third number 5 on one first die and 3 on the second die are opposite to each other.
Rule -3:If there is one element common on both the dice at the different position, then rotate the dice in a clockwise direction to get the opposite surface.
The number ‘2’ is common in both the dice, but it is occurring at a different position. In order to find out, the number appearing on the opposite face, rotate the die in a clockwise direction with the common number as the reference.
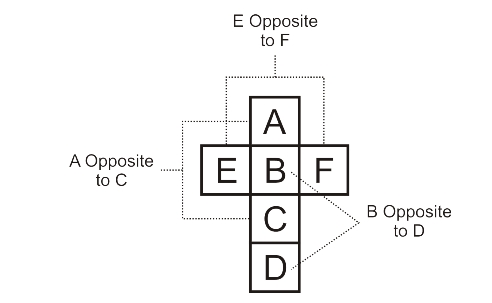
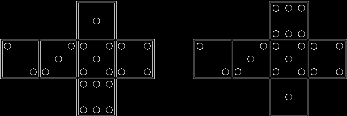
A flat end version of a die
The faces E & F, A & C, B & D are opposite to each other and their surfaces never touch each other.
| Open die | Opposite faces |
|---|---|
1. |
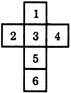1 isopposite to 5 2 is opposite to 4 3 is opposite to 6. |
2. |
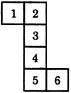1 is opposite to 6 2 is opposite to 4 3 is opposite to 5 |
3. |
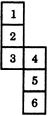1 is opposite to 3 2 is opposite to 5 4 is opposite to 6 |
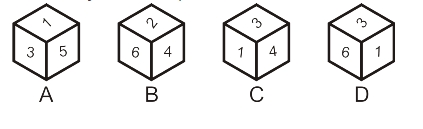
Some examples of Dice :
Example -1:
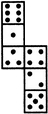
Possible combinations of die. Observe the open die
The number of a possible combination is:
A) Only A
B) Only B
C) Only C
D) Only D
Answer:C) Only C
Explanation:Option 1 is not possible as 3 is not opposed to 5. The second option is also wrong as 2 is not adjacent to 4. Option 3 is possible. And option 4 is not possible as 1 is not adjacent to 6. Hence the correct answer is option 3 i.e. only C.
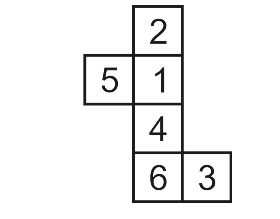
Example -2:
Finding the opposite side. Observe the die
Example -3:
Choose the die that is similar to the die, formed from the open die.
A) Only 1
B) Only 2
C) 1 and 3
D) 1, 2 and 3
Answer:
Explanation:The figure number 1 is possible as the top face is shaded and adjacent faces are blank. Figure 2 is not possible as the surface with a dot should lie between shaded one, but here it is blank. Figure 3 is possible but the 4th one is impossible as the two shaded faces cannot be adjacent to each other. Hence, the correct answer is option C.
Example -4:
How many dots are contained on the face opposite to that containing four dots?
A) 1
B) 2
C) 3
D) 6
Answer:B) 2
Explanation:From the second figure, it can be observed that the face with 4 dots is adjacent to the one with 1 and 5 dots. Hence, then comparing this with the first die it can see that the only place possible the face with 4 dots is opposite it to the face having 2 dots. Hence the correct answer is option B.
Example -5:
Observe the dice.
Example -6:
