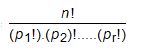Aptitude Permutation and Combination
Permutation
In mathematics, permutation is the different arrangement of a given number of things by taking some or all at a time.
Combination
The combination is a way of selecting items from a collection, such that the order of selection does not matter.
Important formula
Let n be a positive integer. Then, factorial n, denoted n! is defined as:
n! = n(n - 1)(n - 2) ... 3.2.1.
Examples:
- We define 0! = 1.
- 3! = ( 3 x 2 x 1) = 6.
- 4! = (4 x 3 x 2 x 1) = 24.
Number of Permutations:
Number of all permutations of n things, taken r at a time, is given by:
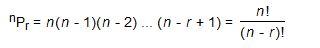
Examples:
- 5P2 = (5 x 4) = 20.
- 4P3 = (4 x 3 x 2) = 24.
Important result
If there are n subjects of which p1 are alike of one kind; p2 are alike of another kind; p3 are alike of third kind and so on and pr are alike of rth kind, such that (p1 + p2 + ... pr) = n.
Then, number of permutations of these n objects is =